Draw a Circle With Two Radii and a Chord

Simple curve of Euclidean geometry

This article is most the shape and mathematical concept. For other uses, see Circle (disambiguation).

Circle
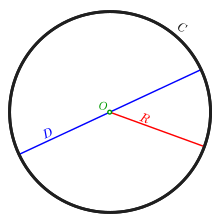A circle (black), which is measured by its circumference (C), bore (D) in blue, and radius (R) in crimson; its center (O) is in light-green.
Type	Conic section
Symmetry group	O(2)
Area	πRtwo
Perimeter	C = 2πR

A circumvolve is a shape consisting of all points in a aeroplane that are at a given distance from a given signal, the centre; equivalently it is the curve traced out by a point that moves in a aeroplane so that its distance from a given point is constant. The distance betwixt any point of the circle and the middle is called the radius. Usually, the radius is required to be a positive number. A circumvolve with ${\displaystyle r=0}$ is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean aeroplane, except where otherwise noted.

Specifically, a circle is a simple closed curve that divides the aeroplane into ii regions: an interior and an exterior. In everyday use, the term "circumvolve" may exist used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circumvolve is only the boundary and the whole figure is called a disc.

A circle may also be defined as a special kind of ellipse in which the two foci are coincident, the eccentricity is 0, and the semi-major and semi-minor axes are equal; or the two-dimensional shape enclosing the virtually area per unit of measurement perimeter squared, using calculus of variations.

Euclid's definition

A circle is a plane figure divisional by ane curved line, and such that all straight lines drawn from a certain indicate within it to the bounding line, are equal. The bounding line is called its circumference and the betoken, its centre.

Topological definition

In the field of topology, a circle isn't limited to the geometric concept, but to all of its homeomorphisms. Two topological circles are equivalent if one can exist transformed into the other via a deformation of R ³ upon itself (known as an ambient isotopy).^[ii]

Terminology

• Annulus: a ring-shaped object, the region divisional by two concentric circles.
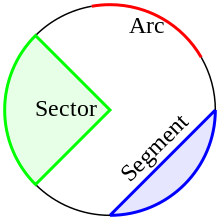
• Arc: whatever continued part of a circle. Specifying 2 stop points of an arc and a eye allows for 2 arcs that together brand upwards a full circle.
• Centre: the signal equidistant from all points on the circle.
• Chord: a line segment whose endpoints prevarication on the circle, thus dividing a circumvolve into two segments.
• Circumference: the length of 1 circuit along the circle, or the altitude around the circumvolve.
• Diameter: a line segment whose endpoints lie on the circle and that passes through the heart; or the length of such a line segment. This is the largest distance betwixt any two points on the circumvolve. It is a special example of a chord, namely the longest chord for a given circle, and its length is twice the length of a radius.
• Disc: the region of the airplane bounded by a circumvolve.
• Lens: the region common to (the intersection of) two overlapping discs.
• Passant: a coplanar directly line that has no point in common with the circle.
• Radius: a line segment joining the centre of a circle with any single point on the circle itself; or the length of such a segment, which is half (the length of) a diameter.
• Sector: a region divisional by 2 radii of equal length with a common center and either of the two possible arcs, determined past this eye and the endpoints of the radii.
• Segment: a region bounded by a chord and one of the arcs connecting the chord'due south endpoints. The length of the chord imposes a lower boundary on the bore of possible arcs. Sometimes the term segment is used simply for regions non containing the center of the circle to which their arc belongs to.
• Secant: an extended chord, a coplanar straight line, intersecting a circumvolve in two points.
• Semicircle: i of the two possible arcs determined by the endpoints of a bore, taking its midpoint as heart. In non-technical common usage information technology may hateful the interior of the two dimensional region bounded by a diameter and one of its arcs, that is technically chosen a half-disc. A half-disc is a special example of a segment, namely the largest i.
• Tangent: a coplanar straight line that has one single point in common with a circumvolve ("touches the circumvolve at this signal").

All of the specified regions may exist considered as open, that is, not containing their boundaries, or equally airtight, including their respective boundaries.

Chord, secant, tangent, radius, and bore

History

The compass in this 13th-century manuscript is a symbol of God'due south act of Cosmos. Detect also the circular shape of the halo.

The word circle derives from the Greek κίρκος/κύκλος (kirkos/kuklos), itself a metathesis of the Homeric Greek κρίκος (krikos), meaning "hoop" or "ring".^[three] The origins of the words circus and circuit are closely related.

Circular slice of silk with Mongol images

The circle has been known since before the beginning of recorded history. Natural circles would have been observed, such equally the Moon, Sun, and a short plant stalk bravado in the wind on sand, which forms a circle shape in the sand. The circle is the footing for the wheel, which, with related inventions such as gears, makes much of mod machinery possible. In mathematics, the study of the circumvolve has helped inspire the development of geometry, astronomy and calculus.

Early scientific discipline, especially geometry and astrology and astronomy, was connected to the divine for most medieval scholars, and many believed that in that location was something intrinsically "divine" or "perfect" that could be found in circles.^{[iv] [five]}

Some highlights in the history of the circumvolve are:

• 1700 BCE – The Rhind papyrus gives a method to find the surface area of a circular field. The result corresponds to 256 / 81 (iii.16049...) as an gauge value of π.^[6]

• 300 BCE – Volume 3 of Euclid's Elements deals with the properties of circles.
• In Plato'southward Seventh Letter there is a detailed definition and explanation of the circle. Plato explains the perfect circle, and how it is different from whatever drawing, words, definition or explanation.
• 1880 CE – Lindemann proves that π is transcendental, effectively settling the millennia-onetime problem of squaring the circle.^[vii]

Analytic results

Circumference

The ratio of a circle's circumference to its diameter is π (pi), an irrational constant approximately equal to three.141592654. Thus the circumference C is related to the radius r and diameter d past:

${\displaystyle C=two\pi r=\pi d.\,}$

Area enclosed

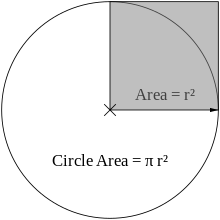
Area enclosed past a circle = π × surface area of the shaded foursquare

Equally proved by Archimedes, in his Measurement of a Circle, the expanse enclosed by a circle is equal to that of a triangle whose base of operations has the length of the circle's circumference and whose height equals the circumvolve's radius,^[8] which comes to π multiplied past the radius squared:

${\displaystyle \mathrm {Area} =\pi r^{2}.\,}$

Equivalently, denoting diameter by d,

${\displaystyle \mathrm {Area} ={\frac {\pi d^{two}}{4}}\approx 0{.}7854d^{2},}$

that is, approximately 79% of the circumscribing square (whose side is of length d).

The circle is the plane curve enclosing the maximum area for a given arc length. This relates the circle to a problem in the calculus of variations, namely the isoperimetric inequality.

Equations

Cartesian coordinates

Circle of radius r = 1, heart (a,b) = (1.2, −0.v)

Equation of a circle

In an x–y Cartesian coordinate system, the circumvolve with center coordinates (a, b) and radius r is the prepare of all points (x, y) such that

${\displaystyle (10-a)^{2}+(y-b)^{two}=r^{ii}.}$

This equation, known as the equation of the circle, follows from the Pythagorean theorem practical to whatever point on the circle: as shown in the adjacent diagram, the radius is the hypotenuse of a right-angled triangle whose other sides are of length |x − a| and |y − b|. If the circle is centred at the origin (0, 0), then the equation simplifies to

${\displaystyle ten^{2}+y^{two}=r^{two}.}$

Parametric grade

The equation tin be written in parametric course using the trigonometric functions sine and cosine as

${\displaystyle ten=a+r\,\cos t,}$

${\displaystyle y=b+r\,\sin t,}$

where t is a parametric variable in the range 0 to 2π, interpreted geometrically equally the angle that the ray from (a,b) to (10,y) makes with the positive x axis.

An alternative parametrisation of the circumvolve is

${\displaystyle x=a+r{\frac {1-t^{2}}{i+t^{ii}}},}$

${\displaystyle y=b+r{\frac {2t}{1+t^{2}}}.}$

In this parameterisation, the ratio of t to r can be interpreted geometrically as the stereographic projection of the line passing through the centre parallel to the ten axis (see Tangent one-half-angle substitution). However, this parameterisation works just if t is fabricated to range not but through all reals simply also to a point at infinity; otherwise, the leftmost signal of the circle would be omitted.

iii-point grade

The equation of the circle adamant past iii points ${\displaystyle (x_{ane},y_{1}),(x_{two},y_{2}),(x_{3},y_{3})}$ not on a line is obtained by a conversion of the 3-indicate form of a circle equation:

${\displaystyle {\frac {({\color {green}10}-x_{1})({\color {greenish}x}-x_{2})+({\color {scarlet}y}-y_{1})({\colour {red}y}-y_{ii})}{({\colour {cherry}y}-y_{ane})({\color {green}ten}-x_{2})-({\colour {red}y}-y_{2})({\colour {green}x}-x_{1})}}={\frac {(x_{three}-x_{1})(x_{3}-x_{ii})+(y_{3}-y_{ane})(y_{three}-y_{two})}{(y_{3}-y_{1})(x_{3}-x_{two})-(y_{3}-y_{2})(x_{3}-x_{1})}}.}$

Homogeneous form

In homogeneous coordinates, each conic section with the equation of a circle has the form

${\displaystyle x^{2}+y^{2}-2axz-2byz+cz^{2}=0.}$

It tin exist proven that a conic section is a circle exactly when it contains (when extended to the circuitous projective airplane) the points I(1: i: 0) and J(1: −i: 0). These points are called the circular points at infinity.

Polar coordinates

In polar coordinates, the equation of a circumvolve is

${\displaystyle r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{2},}$

where a is the radius of the circle, ${\displaystyle (r,\theta )}$ are the polar coordinates of a generic point on the circumvolve, and ${\displaystyle (r_{0},\phi )}$ are the polar coordinates of the centre of the circle (i.e., r ₀ is the distance from the origin to the eye of the circle, and φ is the anticlockwise bending from the positive x axis to the line connecting the origin to the centre of the circle). For a circle centred on the origin, i.e. r ₀ = 0, this reduces to simply r = a . When r ₀ = a , or when the origin lies on the circle, the equation becomes

${\displaystyle r=2a\cos(\theta -\phi ).}$

In the general example, the equation can be solved for r, giving

${\displaystyle r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{two}(\theta -\phi )}}.}$

Note that without the ± sign, the equation would in some cases describe but half a circle.

Circuitous plane

In the complex plane, a circle with a centre at c and radius r has the equation

${\displaystyle |z-c|=r.}$

In parametric course, this can be written as

${\displaystyle z=re^{it}+c.}$

The slightly generalised equation

${\displaystyle pz{\overline {z}}+gz+{\overline {gz}}=q}$

for real p, q and complex k is sometimes chosen a generalised circle. This becomes the above equation for a circle with ${\displaystyle p=one,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}}$ , since ${\displaystyle |z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}}$ . Non all generalised circles are actually circles: a generalised circle is either a (true) circumvolve or a line.

Tangent lines

The tangent line through a signal P on the circumvolve is perpendicular to the diameter passing through P. If P = (x _one, y ₁) and the circle has centre (a, b) and radius r, and so the tangent line is perpendicular to the line from (a, b) to (x _one, y ₁), so it has the form (x _i − a)x + (y _ane – b)y = c . Evaluating at (x ₁, y ₁) determines the value of c, and the event is that the equation of the tangent is

${\displaystyle (x_{1}-a)ten+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{i}-b)y_{one},}$

or

${\displaystyle (x_{i}-a)(x-a)+(y_{1}-b)(y-b)=r^{two}.}$

If y ₁ ≠ b , then the slope of this line is

${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{one}-a}{y_{one}-b}}.}$

This can besides be found using implicit differentiation.

When the centre of the circumvolve is at the origin, then the equation of the tangent line becomes

${\displaystyle x_{ane}x+y_{1}y=r^{2},}$

and its gradient is

${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}}{y_{1}}}.}$

Properties

• The circumvolve is the shape with the largest area for a given length of perimeter (meet Isoperimetric inequality).
• The circle is a highly symmetric shape: every line through the centre forms a line of reflection symmetry, and it has rotational symmetry around the eye for every bending. Its symmetry group is the orthogonal group O(ii,R). The group of rotations solitary is the circle group T.
• All circles are similar.
  • A circle circumference and radius are proportional.
  • The area enclosed and the square of its radius are proportional.
  • The constants of proportionality are 2π and π respectively.
• The circle that is centred at the origin with radius 1 is called the unit circumvolve.
  • Thought of every bit a bully circle of the unit of measurement sphere, it becomes the Riemannian circle.
• Through whatsoever three points, not all on the same line, at that place lies a unique circumvolve. In Cartesian coordinates, it is possible to requite explicit formulae for the coordinates of the centre of the circumvolve and the radius in terms of the coordinates of the three given points. See circumcircle.

Chord

• Chords are equidistant from the centre of a circle if and only if they are equal in length.
• The perpendicular bisector of a chord passes through the center of a circumvolve; equivalent statements stemming from the uniqueness of the perpendicular bisector are:
  • A perpendicular line from the center of a circumvolve bisects the chord.
  • The line segment through the center bisecting a chord is perpendicular to the chord.
• If a central angle and an inscribed angle of a circle are subtended by the same chord and on the same side of the chord, then the central angle is twice the inscribed bending.
• If two angles are inscribed on the same chord and on the same side of the chord, then they are equal.
• If 2 angles are inscribed on the same chord and on reverse sides of the chord, and so they are supplementary.
  • For a circadian quadrilateral, the exterior bending is equal to the interior opposite bending.
• An inscribed angle subtended by a bore is a correct angle (encounter Thales' theorem).
• The bore is the longest chord of the circle.
  • Amongst all the circles with a chord AB in common, the circle with minimal radius is the i with diameter AB.
• If the intersection of any two chords divides 1 chord into lengths a and b and divides the other chord into lengths c and d, then ab = cd .
• If the intersection of whatsoever 2 perpendicular chords divides one chord into lengths a and b and divides the other chord into lengths c and d, and then a ^two + b ² + c ² + d ⁱⁱ equals the square of the diameter.^[9]
• The sum of the squared lengths of whatever ii chords intersecting at right angles at a given point is the same as that of any other two perpendicular chords intersecting at the same point and is given by eightr ² − ivp ², where r is the circumvolve radius, and p is the altitude from the centre point to the point of intersection.^[ten]
• The altitude from a point on the circle to a given chord times the diameter of the circle equals the product of the distances from the point to the ends of the chord.^{[11] : p.71}

Tangent

• A line drawn perpendicular to a radius through the end signal of the radius lying on the circumvolve is a tangent to the circle.
• A line drawn perpendicular to a tangent through the signal of contact with a circle passes through the centre of the circle.
• Two tangents can always be drawn to a circle from any point outside the circle, and these tangents are equal in length.
• If a tangent at A and a tangent at B intersect at the exterior point P, then denoting the centre as O, the angles ∠BOA and ∠BPA are supplementary.
• If AD is tangent to the circle at A and if AQ is a chord of the circle, and then ∠DAQ = one / 2 arc(AQ).

Theorems

• The chord theorem states that if two chords, CD and EB, intersect at A, then AC × AD = AB × AE .
• If two secants, AE and AD, also cut the circle at B and C respectively, and so Air-conditioning × AD = AB × AE (corollary of the chord theorem).
• A tangent tin exist considered a limiting example of a secant whose ends are coincident. If a tangent from an external bespeak A meets the circle at F and a secant from the external bespeak A meets the circle at C and D respectively, and then AF ² = AC × AD (tangent–secant theorem).
• The angle betwixt a chord and the tangent at i of its endpoints is equal to one half the angle subtended at the eye of the circle, on the reverse side of the chord (tangent chord angle).
• If the angle subtended past the chord at the eye is xc°, and so ℓ = r √2 , where ℓ is the length of the chord, and r is the radius of the circle.
• If ii secants are inscribed in the circle as shown at right, and then the measurement of angle A is equal to ane one-half the difference of the measurements of the enclosed arcs ( ${\displaystyle {\overset {\frown }{DE}}}$ and ${\displaystyle {\overset {\pout }{BC}}}$ ). That is, ${\displaystyle 2\angle {CAB}=\bending {DOE}-\angle {BOC}}$ , where O is the center of the circle (secant–secant theorem).

Inscribed angles

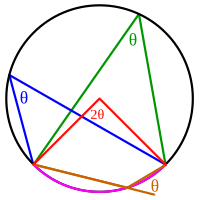
An inscribed angle (examples are the blue and green angles in the figure) is exactly half the corresponding cardinal angle (ruddy). Hence, all inscribed angles that subtend the same arc (pink) are equal. Angles inscribed on the arc (brown) are supplementary. In particular, every inscribed angle that subtends a diameter is a right angle (since the central angle is 180°).

Sagitta

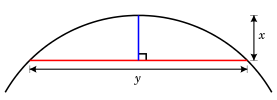
The sagitta is the vertical segment.

The sagitta (also known as the versine) is a line segment drawn perpendicular to a chord, betwixt the midpoint of that chord and the arc of the circle.

Given the length y of a chord and the length ten of the sagitta, the Pythagorean theorem tin can exist used to summate the radius of the unique circle that will fit around the ii lines:

${\displaystyle r={\frac {y^{ii}}{8x}}+{\frac {10}{2}}.}$

Another proof of this consequence, which relies only on two chord properties given above, is as follows. Given a chord of length y and with sagitta of length x, since the sagitta intersects the midpoint of the chord, nosotros know that information technology is a part of a diameter of the circle. Since the diameter is twice the radius, the "missing" part of the bore is (2r − x ) in length. Using the fact that one role of one chord times the other part is equal to the same product taken along a chord intersecting the first chord, we find that (2r − 10)x = (y / 2)² . Solving for r, we find the required consequence.

Compass and straightedge constructions

There are many compass-and-straightedge constructions resulting in circles.

The simplest and well-nigh basic is the construction given the heart of the circumvolve and a betoken on the circle. Place the stock-still leg of the compass on the middle indicate, the movable leg on the point on the circle and rotate the compass.

Structure with given diameter

• Construct the midpoint Thou of the diameter.
• Construct the circle with centre 1000 passing through one of the endpoints of the diameter (it volition also pass through the other endpoint).

Construct a circle through points A, B and C past finding the perpendicular bisectors (red) of the sides of the triangle (blue). Merely two of the iii bisectors are needed to observe the centre.

Construction through three noncollinear points

• Proper name the points P , Q and R ,
• Construct the perpendicular bisector of the segment PQ .
• Construct the perpendicular bisector of the segment PR .
• Label the point of intersection of these two perpendicular bisectors M . (They meet because the points are non collinear).
• Construct the circle with centre M passing through i of the points P , Q or R (it will also laissez passer through the other 2 points).

Circle of Apollonius

Apollonius' definition of a circumvolve: d ₁/d _two abiding

Apollonius of Perga showed that a circle may also be divers as the set of points in a plane having a constant ratio (other than ane) of distances to two fixed foci, A and B.^{[12] [13]} (The set of points where the distances are equal is the perpendicular bisector of segment AB, a line.) That circle is sometimes said to be fatigued virtually two points.

The proof is in two parts. First, i must prove that, given 2 foci A and B and a ratio of distances, whatever bespeak P satisfying the ratio of distances must fall on a detail circle. Allow C exist some other point, also satisfying the ratio and lying on segment AB. Past the angle bisector theorem the line segment PC volition bisect the interior angle APB, since the segments are similar:

${\displaystyle {\frac {AP}{BP}}={\frac {Air conditioning}{BC}}.}$

Analogously, a line segment PD through some point D on AB extended bisects the corresponding exterior angle BPQ where Q is on AP extended. Since the interior and outside angles sum to 180 degrees, the angle CPD is exactly 90 degrees; that is, a right angle. The set of points P such that angle CPD is a right angle forms a circle, of which CD is a diameter.

2nd, see^{[14] : p.15} for a proof that every point on the indicated circle satisfies the given ratio.

Cross-ratios

A closely related property of circles involves the geometry of the cross-ratio of points in the complex airplane. If A, B, and C are every bit above, then the circle of Apollonius for these iii points is the drove of points P for which the absolute value of the cross-ratio is equal to one:

${\displaystyle {\large |}[A,B;C,P]{\large |}=1.}$

Stated another way, P is a point on the circle of Apollonius if and just if the cross-ratio [A, B; C, P] is on the unit circle in the complex aeroplane.

Generalised circles

If C is the midpoint of the segment AB, and then the drove of points P satisfying the Apollonius condition

${\displaystyle {\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}}$

is not a circumvolve, but rather a line.

Thus, if A, B, and C are given singled-out points in the plane, then the locus of points P satisfying the to a higher place equation is called a "generalised circle." It may either exist a true circle or a line. In this sense a line is a generalised circle of infinite radius.

Inscription in or circumscription about other figures

In every triangle a unique circle, called the incircle, can exist inscribed such that information technology is tangent to each of the iii sides of the triangle.^[15]

Nearly every triangle a unique circle, called the circumcircle, can be circumscribed such that it goes through each of the triangle's three vertices.^[16]

A tangential polygon, such equally a tangential quadrilateral, is any convex polygon within which a circumvolve tin can be inscribed that is tangent to each side of the polygon.^[17] Every regular polygon and every triangle is a tangential polygon.

A circadian polygon is any convex polygon about which a circle can be circumscribed, passing through each vertex. A well-studied example is the cyclic quadrilateral. Every regular polygon and every triangle is a cyclic polygon. A polygon that is both circadian and tangential is called a bicentric polygon.

A hypocycloid is a curve that is inscribed in a given circle past tracing a fixed point on a smaller circle that rolls within and tangent to the given circle.

Limiting case of other figures

The circle can exist viewed as a limiting case of each of various other figures:

• A Cartesian oval is a set of points such that a weighted sum of the distances from any of its points to 2 fixed points (foci) is a abiding. An ellipse is the case in which the weights are equal. A circumvolve is an ellipse with an eccentricity of zero, pregnant that the ii foci coincide with each other every bit the centre of the circle. A circle is also a different special case of a Cartesian oval in which one of the weights is zero.
• A superellipse has an equation of the form ${\displaystyle \left|{\frac {x}{a}}\right|^{northward}\!+\left|{\frac {y}{b}}\right|^{n}\!=1}$ for positive a, b, and n. A supercircle has b = a . A circle is the special example of a supercircle in which n = 2.
• A Cassini oval is a fix of points such that the product of the distances from any of its points to 2 fixed points is a constant. When the 2 fixed points coincide, a circle results.
• A curve of constant width is a figure whose width, defined as the perpendicular altitude betwixt two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines. The circumvolve is the simplest case of this type of effigy.

In other p-norms

Illustrations of unit circles (come across also superellipse) in different p -norms (every vector from the origin to the unit circle has a length of i, the length being calculated with length-formula of the corresponding p ).

Defining a circumvolve as the set up of points with a fixed distance from a point, different shapes tin can be considered circles under different definitions of altitude. In p-norm, altitude is determined by

${\displaystyle \left\|x\correct\|_{p}=\left(|x_{1}|^{p}+|x_{two}|^{p}+\dotsb +|x_{n}|^{p}\right)^{1/p}.}$

In Euclidean geometry, p = 2, giving the familiar

${\displaystyle \left\|x\right\|_{ii}={\sqrt {|x_{1}|^{2}+|x_{ii}|^{2}+\dotsb +|x_{north}|^{2}}}.}$

In taxicab geometry, p = i. Taxicab circles are squares with sides oriented at a 45° angle to the coordinate axes. While each side would have length ${\displaystyle {\sqrt {ii}}r}$ using a Euclidean metric, where r is the circle'southward radius, its length in taxicab geometry is 2r. Thus, a circle's circumference is 8r. Thus, the value of a geometric analog to ${\displaystyle \pi }$ is 4 in this geometry. The formula for the unit of measurement circumvolve in taxicab geometry is ${\displaystyle |x|+|y|=1}$ in Cartesian coordinates and

${\displaystyle r={\frac {i}{|\sin \theta |+|\cos \theta |}}}$

in polar coordinates.

A circle of radius 1 (using this distance) is the von Neumann neighborhood of its middle.

A circumvolve of radius r for the Chebyshev distance (L_∞ metric) on a plane is also a square with side length 2r parallel to the coordinate axes, so planar Chebyshev distance tin can exist viewed every bit equivalent past rotation and scaling to planar taxicab distance. Yet, this equivalence between Fifty₁ and L_∞ metrics does not generalize to higher dimensions.

Locus of abiding sum

Consider a finite set of ${\displaystyle n}$ points in the plane. The locus of points such that the sum of the squares of the distances to the given points is constant is a circumvolve, whose middle is at the centroid of the given points.^[18] A generalization for higher powers of distances is obtained if under ${\displaystyle n}$ points the vertices of the regular polygon ${\displaystyle P_{due north}}$ are taken.^[xix] The locus of points such that the sum of the ${\displaystyle (2m)}$ -thursday power of distances ${\displaystyle d_{i}}$ to the vertices of a given regular polygon with circumradius ${\displaystyle R}$ is abiding is a circle, if

${\displaystyle \sum _{i=1}^{n}d_{i}^{2m}>nR^{2m}}$ , where ${\displaystyle one thousand}$ =ane,ii,…, ${\displaystyle n}$ -i;

whose center is the centroid of the ${\displaystyle P_{n}}$ .

In the case of the equilateral triangle, the loci of the abiding sums of the second and fourth powers are circles, whereas for the foursquare, the loci are circles for the constant sums of the 2d, quaternary, and sixth powers. For the regular pentagon the constant sum of the 8th powers of the distances volition be added and then forth.

Squaring the circle

Squaring the circumvolve is the problem, proposed by ancient geometers, of constructing a square with the same area as a given circle past using simply a finite number of steps with compass and straightedge.

In 1882, the task was proven to be incommunicable, every bit a issue of the Lindemann–Weierstrass theorem, which proves that pi (π) is a transcendental number, rather than an algebraic irrational number; that is, information technology is not the root of any polynomial with rational coefficients. Despite the impossibility, this topic continues to be of involvement for pseudomath enthusiasts.

Significance in art and symbolism

From the time of the earliest known civilisations – such as the Assyrians and ancient Egyptians, those in the Indus Valley and along the Yellow River in China, and the Western civilisations of ancient Hellenic republic and Rome during classical Antiquity – the circle has been used directly or indirectly in visual art to convey the artist'due south message and to express certain ideas. Yet, differences in worldview (beliefs and culture) had a great impact on artists' perceptions. While some emphasised the circle'southward perimeter to demonstrate their autonomous manifestation, others focused on its centre to symbolise the concept of cosmic unity. In mystical doctrines, the circumvolve mainly symbolises the infinite and cyclical nature of existence, only in religious traditions information technology represents heavenly bodies and divine spirits. The circle signifies many sacred and spiritual concepts, including unity, infinity, wholeness, the universe, divinity, balance, stability and perfection, amongst others. Such concepts have been conveyed in cultures worldwide through the use of symbols, for example, a compass, a halo, the vesica piscis and its derivatives (fish, eye, aureole, mandorla, etc.), the ouroboros, the Dharma bicycle, a rainbow, mandalas, rose windows and so along.^[20]

See besides

References

1. ^ OL 7227282M
2. ^ Gamelin, Theodore (1999). Introduction to topology . Mineola, N.Y: Dover Publications. ISBN0486406806.
3. ^ krikos Archived 2013-xi-06 at the Wayback Machine, Henry George Liddell, Robert Scott, A Greek-English language Dictionary, on Perseus
4. ^ Arthur Koestler, The Sleepwalkers: A History of Human's Changing Vision of the Universe (1959)
5. ^ Proclus, The Vi Books of Proclus, the Platonic Successor, on the Theology of Plato Archived 2017-01-23 at the Wayback Car Tr. Thomas Taylor (1816) Vol. ii, Ch. two, "Of Plato"
6. ^ Chronology for 30000 BC to 500 BC Archived 2008-03-22 at the Wayback Auto. History.mcs.st-andrews.air-conditioning.britain. Retrieved on 2012-05-03.
7. ^ Squaring the circle Archived 2008-06-24 at the Wayback Machine. History.mcs.st-andrews.ac.uk. Retrieved on 2012-05-03.
8. ^ Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison Wesley Longman, p. 108, ISBN978-0-321-01618-8
9. ^ Posamentier and Salkind, Challenging Problems in Geometry, Dover, 2d edition, 1996: pp. 104–105, #4–23.
10. ^ College Mathematics Journal 29(four), September 1998, p. 331, trouble 635.
11. ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007.
12. ^ Harkness, James (1898). "Introduction to the theory of analytic functions". Nature. 59 (1530): thirty. Bibcode:1899Natur..59..386B. doi:x.1038/059386a0. S2CID 4030420. Archived from the original on 2008-10-07.
13. ^ Ogilvy, C. Stanley, Excursions in Geometry, Dover, 1969, 14–17.
14. ^ Altshiller-Court, Nathan, College Geometry, Dover, 2007 (orig. 1952).
15. ^ Incircle – from Wolfram MathWorld Archived 2012-01-21 at the Wayback Machine. Mathworld.wolfram.com (2012-04-26). Retrieved on 2012-05-03.
16. ^ Circumcircle – from Wolfram MathWorld Archived 2012-01-20 at the Wayback Car. Mathworld.wolfram.com (2012-04-26). Retrieved on 2012-05-03.
17. ^ Tangential Polygon – from Wolfram MathWorld Archived 2013-09-03 at the Wayback Auto. Mathworld.wolfram.com (2012-04-26). Retrieved on 2012-05-03.
18. ^ Apostol, Tom; Mnatsakanian, Mamikon (2003). "Sums of squares of distances in 1000-infinite". American Mathematical Monthly. 110 (six): 516–526. doi:ten.1080/00029890.2003.11919989. S2CID 12641658.
19. ^ Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. eleven: 335–355. arXiv:2010.12340.
20. ^ Abdullahi, Yahya (October 29, 2019). "The Circle from East to West". In Charnier, Jean-François (ed.). The Louvre Abu Dhabi: A World Vision of Art. Rizzoli International Publications, Incorporated. ISBN9782370741004.

Farther reading

• Pedoe, Dan (1988). Geometry: a comprehensive course . Dover. ISBN9780486658124.
• "Circle" in The MacTutor History of Mathematics annal

External links

Wikiquote has quotations related to: Circles

• "Circumvolve", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Circle at PlanetMath.
• Weisstein, Eric W. "Circumvolve". MathWorld.
• "Interactive Coffee applets". for the properties of and elementary constructions involving circles
• "Interactive Standard Form Equation of Circle". Click and drag points to see standard form equation in action
• "Munching on Circles". cutting-the-knot

dillarduncerced.blogspot.com

Source: https://en.wikipedia.org/wiki/Circle